This article has been originally published as part of the column FABBRICATION in XXI magazine, vol.161, July/August 2017. This article can be accessed here in Turkish.

Alberti’s computational communication, Gaudi’s informational models, Otto’s free structural experimentations. All share the same roots. Collage by Efe Gözen, 2017.
Many believe the emergence of computational design corresponds to the golden era of the digital age – last decade of the 20th century and the first decade of the 21st century when computers became excessively accessible and computational power is in abundance. Among the many, a hefty majority would argue that the heydays of Grasshopper marks the new age. After all, it was in 2008 when Patrik Schumacher had heralded the arrival of Parametricism as the great new style after Modernism1– one and only savior of architecture in distress. Some would argue that it was Frank Gehry, Greg Lynn or Branko Kolarevic who first pushed the limits of computers in design in ‘90s. Fewer, who have realized that computational architecture has nothing to do with computers, would contend it was Frei Otto and his experimental models that defined computational thinking in architecture. Amongst the few who are into early modernism would recognize that Antoni Gaudi’s catenary arch models were the first structurally informed models of its time and thus claim him as the first pioneer in computational design.
Yet, all would be wrong. Preceding Gaudi merely by more than four hundred years, Leon Battista Alberti can be regarded as the first documented polymath architect who embraced computational way of thinking. We have been hinting2 there was more to Alberti in addition to defining the role of the architect, and the time has come to expand his approach to design.
We had mentioned that Alberti believed the architect should be separated from the builder and should be free to design for any building material and to use any technical device that would make his building stand. As he epitomized the Renaissance Man – author, artist, architect, poet, priest, linguist, philosopher and cryptographer; his mindset was transdisciplinary and the technical devices at his disposal were diverse. He fused tools of various backgrounds into one another in order to address complex problems with multidisciplinary backgrounds. This was most evident in cases whenever precise reproduction was of the essence. As he placed architect separate from the builder, he tried to overcome the newly formed communication gap through mixing the alphabet, the diagram and the algorithm – substituting non-transmissible pictures.3 This has even reflected on his general form of communication devoid time. Lack of illustrations in his three famous treatises on painting, architecture, and sculpture is noteworthy. Rather, he digitized his form of communication replacing all that was analogue with a list of numbers and a set of computational instructions.
In Descriptio urbis Romae, Alberti has digitized the map of Rome using a system of polar coordinates. The book is the description of a specific tool developed by Alberti and a list of numbers. Feeding these numbers into the tool, one could recreate the map of Rome in any scale he wishes depending on the size of the tool as the polar coordinate enabled scalable vector drawings. The book was the grandfather of all digital CAD drawings in architecture, a codified set of instructions which could be repeated to create same results or modified to obtain derivatives. The idea for the tool certainly was not novel, as Ptolemy proposed it thirteen centuries earlier – although, it was the first documented use of the method complete with the description for the realization of the tool and the data for the recreation of the information.
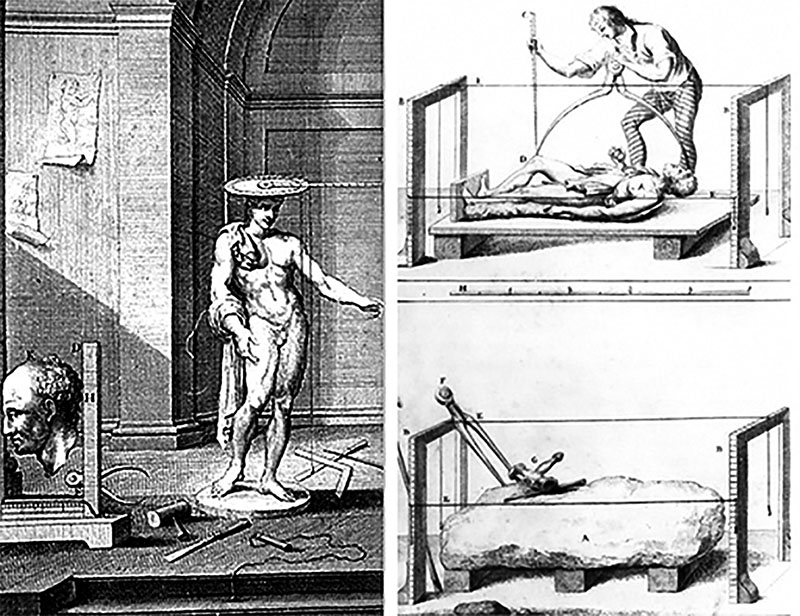
The five century year old F2F CAD-CAM technology, enhanced with analogue 3D scanning. We hope Alberti excuses our use of illustrations in order to appeal to a larger audience.
Alberti surpassed the original methodology as he applied the same principle to three-dimensional objects. In his treatise on sculpture, De Statua, he has prescribed a method to scan human body and translate it into a list of three-dimensional coordinates. Similar to the previous tool he utilized for 2D polar coordinates, a revolving instrument was placed on the head of the subject and a plumb was placed to measure points in all coordinates. Just like the 3D scanning technology of today, Alberti was recreating the point-cloud of the subject for replication ad infinitum in a variable scale, for any time and place. Alberti invented the file-to-factory (F2F) CAD-CAM in 15th century, five centuries earlier than the invention of C in CAD/CAM.
Fast forward 400 years, a Catalan Modernista by the name Antoni Gaudi preferred to use informational models and diagrams as design tools. The ‘old vault theory’ he applied is based on finding equilibrium configuration. The informational model is the real world application of Robert Hooke’s and Guttfried Wilhelm Leibniz’s treatises on catenary arches. The major component of the physical model is a chain suspended from both its ends resulting in a catenary curve that naturally distributes the static load (in this case tension) evenly between the links of the chain. When this configuration is flipped vertically and it is materialized with brick or stone, the static load acts in compression resulting in an optimally efficient arch.4 Through experimentation with these models, he discovered a way to use traditional Catalan masonry techniques in novel ways. The large open layouts, spacious halls, and intricate structural geometry that awe us in his buildings are the outcome of this technique.

The inverted relaxed catenary arches result in the final iteration of the original design of the church for the Colonia Güell.
The physical models allowed him to explore endless iterations of organic forms, since every adjustment would immediately trigger the physical re-computation of optimal arches he built. Speaking of these adjustments, one of the features of so-called parametric design software is that it updates a complete three-dimensional digital model any time a parameter is altered. Gaudi’s hanging chains do exactly that: if a chain end-point is moved so as to enlarge or reduce, say, the floor plan in one corner, then the shape of the entire hanging chain model shifts and settles into a newly optimized catenary geometry.
Computational design process Gaudi effectively invented long before the invention of computer allowed his successors to understand his approach towards design and fabrication. Although he spent over 40 years to design La Sagrada Familia, he had only finished the first order of the geometry, which are the curves of the catenary arch and had never applied any of the second order geometry (ruled surfaces) to masonry construction in the way he proposed with his scale models. Today, one would say that there is no possibility of simply extrapolating from where he left off. The conundrum he left behind is still carried out today by his successors, a team led by Mark Burry. Given that the building is so manifestly complex, it seems extraordinary that he succeeded in leaving behind a codex sufficiently comprehensive that the project could be constructed forward and is on its path for completion.5
Most prominent contemporary architect to explore architectural design through informational modeling was Frei Otto. Beginning his experimentations with soap film models in 1961, he suspended soap film and dropped looped strings which he later pulled to form the minimal surface in between the loop as the surface tension minimized to find equilibrium for the final form. Further control over the surface was possible using custom forks to introduce openings and custom needles or knobs to manipulate the surface topography.
Otto founded the Institute for Lightweight Structures at the University of Stuttgart in 1964, and he led the design for the Expo 1967 in Montreal. It was a refreshing take on the pavilion design, breaking the orthogonal volumes to create novel spatial relations regarding the air and the light. As the method was a proven success, he was assigned to undertake a much more ambitious project with Günther Behnisch: the design of the Munich Olympic Stadium. The stadium roof was designed similar to his previous approach with soap films, and built in scale with appropriate loads for simulation which was closely monitored with a series of cameras.

Informational model for the roof structure of Munich Olympic Stadium. The scale model for the tensile structure is closely monitored with cameras.
Even though he has utilized computers extensively for the calculation of these structure, Otto believed the utmost necessity of free experimentation in the analogue world. He believed;
The computer can only calculate what is already conceptually inside of it; you can only find what you look for in computers. Nevertheless, you can find what you haven’t searched for with free experimentation.Frei Otto
Alberti reinvented the relation between the alphabet, the diagram and the algorithm to develop analogue computational communication. Building upon this mode of communication, Gaudi utilized informational models to design the building process of a manifestly complex building which would be impossible to document with orthodox methods. Otto pushed this notion further to exploit chance encounters for free experimentation. Computational thinking precedes the digital, as computers are not the key component of computational design. Are there no cases where they are indispensable to the process? Well, let’s discuss that after summer.
- Schumacher, P. (2008) Parametricism as Style – Parametricist Manifesto
- For more on the topic, please refer to helloWorld published in 2017 February XXI
- Carpo, M. (2011). The Alphabet and the Algorithm. Cambridge: MIT Press.
- Huerta, S. “Structural design in the work of Gaudi.” Architectural science review 49.4 (2006): 324-339.
- Burry, M. “Antoni Gaudi’s Computational Legacy.” Human Centric Computing Languages and Environments, 2003. Proceedings. 2003 IEEE Symposium on. IEEE, 2003.
- Songel, J.M. (2010). A Conversation with Frei Otto. New Jersey: Stanford Architectural Press.
